7 min read
All about databases

Photo by Victor Moriyama
What is a database?
Data → information, Base → platform
A platform for storing data in a structured format for accessing, manipulation and analysis purposes.
Types
What is a DBMS ?
Provides tools to enable users to perform CRUD operations, along with index management, data security, etc.
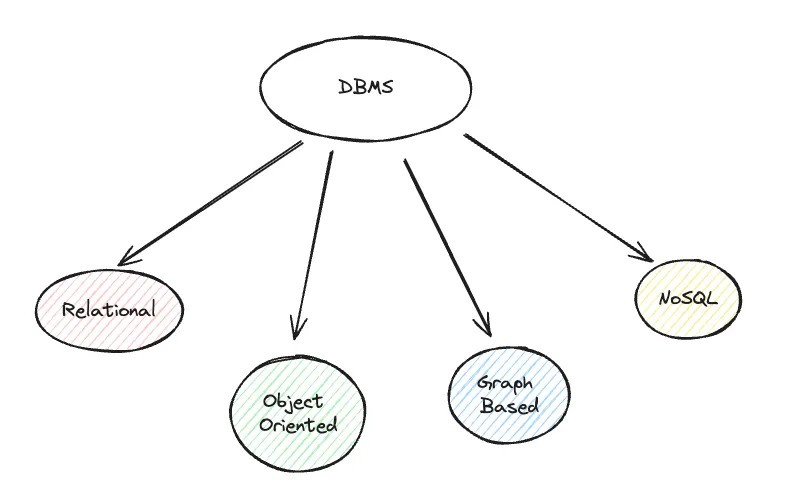
Relational DBMS
A type of database that stores and provides access to data points that are related to one another.
Here the relational model means that logical structures (tables, views, indexes) are separate from physical storage.
How does database store data internally
Internal design strategies employed by databases to optimise operations, along with their advantages and disadvantages.
Traditional relational databases store data in a B-Tree structures on disk, indexes are also maintained for this data in B-Tree format as well for faster access of data.
Disk Structure
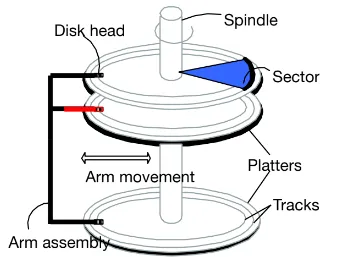
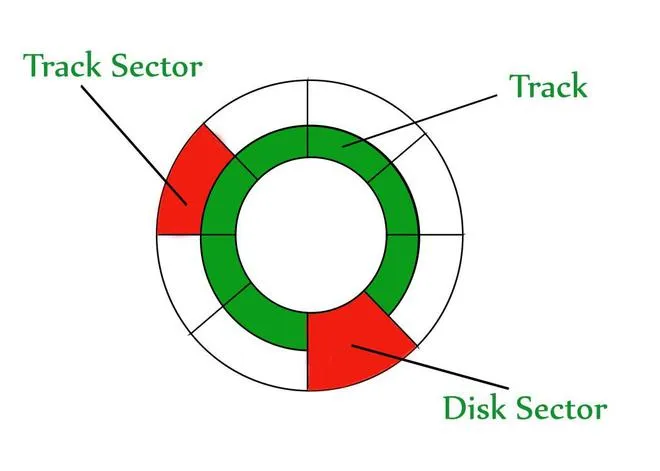
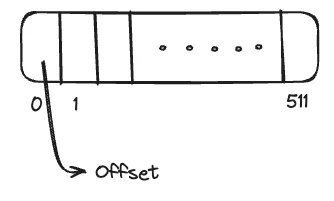
How data is organised on the disk
Let each row size of the table is X bytes. No. of records per block = 512 / X
If we have Y rows then => (X*Y / 512) blocks are required. If we access entire table then we need to traverse more blocks hence more time. Also if we search for a particular row then too we have to check at-most (X*Y / 512) blocks.
We can reduce this time by adding indexes, which will in-turn have the block address of the record/row for which the column index is applied. For each row we will have entry inside index table.
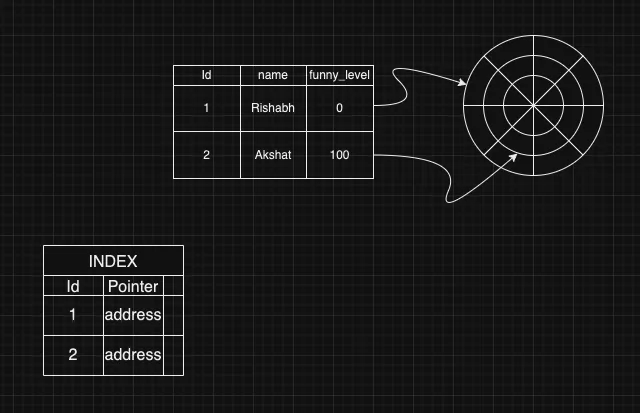
This index table (dense index) is also stored on the disk. How much space would index take? Let’s say Id has a bytes and pointer is of b bytes => (a+b) total bytes for one row, which is way less than X (size of one row in database).
Hence for Y entries, blocks required for index table = (Y*(a+b))/512. Therefore now whenever we need to search at-most (Y*(a+b))/512 blocks would be traversed for index and 1 block for that key that is to be searched, therefore ((Y*(a+b))/512) +1 at-most blocks.
Multilevel Indexing
As the size of the table grows the index table would are require more blocks on the disk, this would increase search time in index itself. Solution → We can have index on the index table ( sorry :) ).
Since the index table is stored in (Y(a+b))/512* blocks, the new table pointer will point to which block the index would be present.
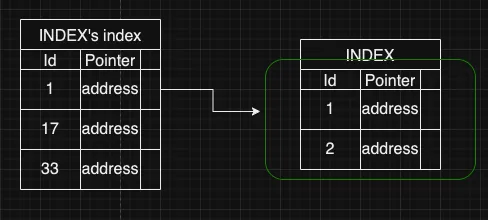
This new index table would be sparse index (not all values are present). This can make your search really fast. We can go on to make more indexes on the index table resulting in a tree structure.
Similar to binary search trees there are M-way search trees where keys are M-1 and at-most M children. Insertion is insufficient in M-way search tree which can result in maximum of N nodes for N keys. There are some rules on insertion in M-way search trees that are called B-trees.
The rows we insert are leaf of B-tree. Index to these data in B Tree structure mostly in RAM to guarantee faster access to the original data. When the data is too large and RAM is out of space then database will read from the disk. Disk I/O is very costly, B Tree is a random read/write, in-place replacement, very compact & self balancing data structure which suffers from disk I/O limitation.
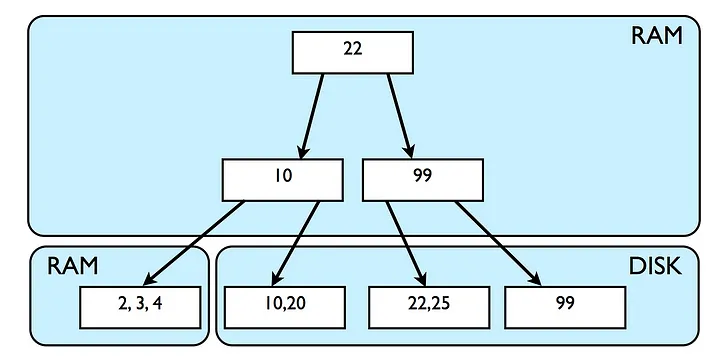
If the block size is 16KB (MySQL), for read or write data to the database, a block of disk pages of size 16 KB will be fetched from the disk into RAM, it will get manipulated and then written back to disk again if required. As mentioned earlier, leaves of a B Tree reside at the same level, it takes O(logN) steps to search a data in B Tree ordered by primary key.
However write operations are worse. You can write hardly 100 bytes/second in a random write fashion. Scaling read operations can often be straightforward depending on the specific use case, achieved through methods such as caching, implementing search indexes, or allocating additional memory. However, scaling write operations can be challenging. When dealing with the need to write or update large volumes of data within a database, relying solely on B-tree structures may prove inadequate.
LSM (Log Structured Merge Tree)
a.k.a. the secret sauce 🥫 behind NoSQL
— In this system, unlike B Tree, there is no in-place replacement of data i.e; once data is written to some portion in the disk, it never gets modified.
— It’s like logging the data sequentially somewhere. Hence the term ‘Log Structured’ comes into picture.
Hardware
— Traditional magnetic hard drives can write data upto 100 MB/second.
— Modern SSD drives can write far more in a sequential manner.
— In fact SSD drives have some internal parallelism mechanism where they can write 16 to 32 MB data together on itself at once.
— LSM tree is very suitable match for SSD (Sequential write)
Cassandra or any LSM system maintains one or more in-memory data structure.
( in the below image Memtable ) like self balancing trees
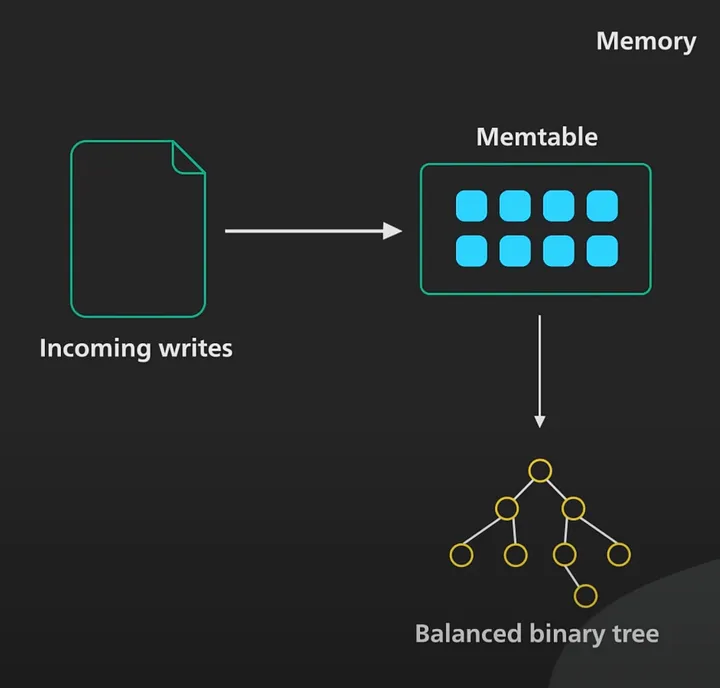
When memtable contents exceed a configurable threshold, the memtable data is put in a queue to be flushed to disk.
To flush the data, Cassandra writes sorted data to disk sequentially.
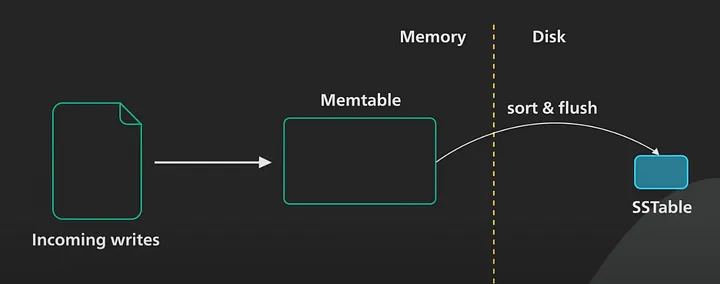
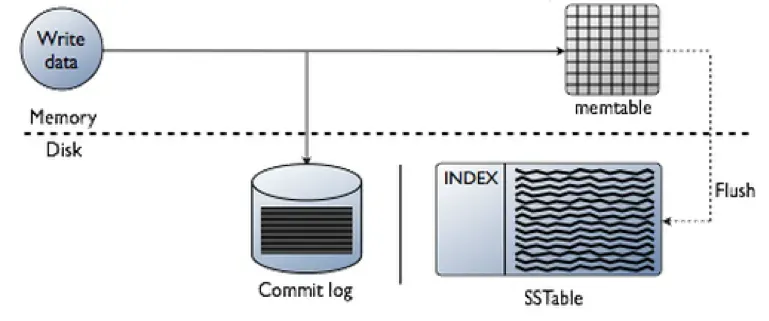
SSTables are immutable
LSM systems can maintain multiple such files on disk
— If a data is not found in memtable, Cassandra needs to scan all the on-disk SSTables as the data may be scattered across all the SSTables.
— Cassandra reads are slower than writes.
Improvement?
Compaction
— LSM system runs compaction process continuously in the background to minimize number of such SSTables.
— Applies merge sort on SSTables and writes the new sorted data in a new SSTable and deletes old SSTables.
Sometimes compaction cannot keep up with the amount of data writes
Probabilistic Data Structures
In order to make read faster, LSM systems keep up many tasks and workarounds like Bloom filters
So some probabilistic data structures like Bloom filters are used to get the idea if some data exists in a SSTable in constant time.
Bloom Filters
Anything between B Tree & LSM Tree and give us okayish read write speed?
Fractal tree
— Similar to B tree but optimizations to make it fast.
— Fractal tree supports message buffers inside all nodes except leaf nodes.
— Patent with TokuDB (block size → 4MB)
Writes / Reads
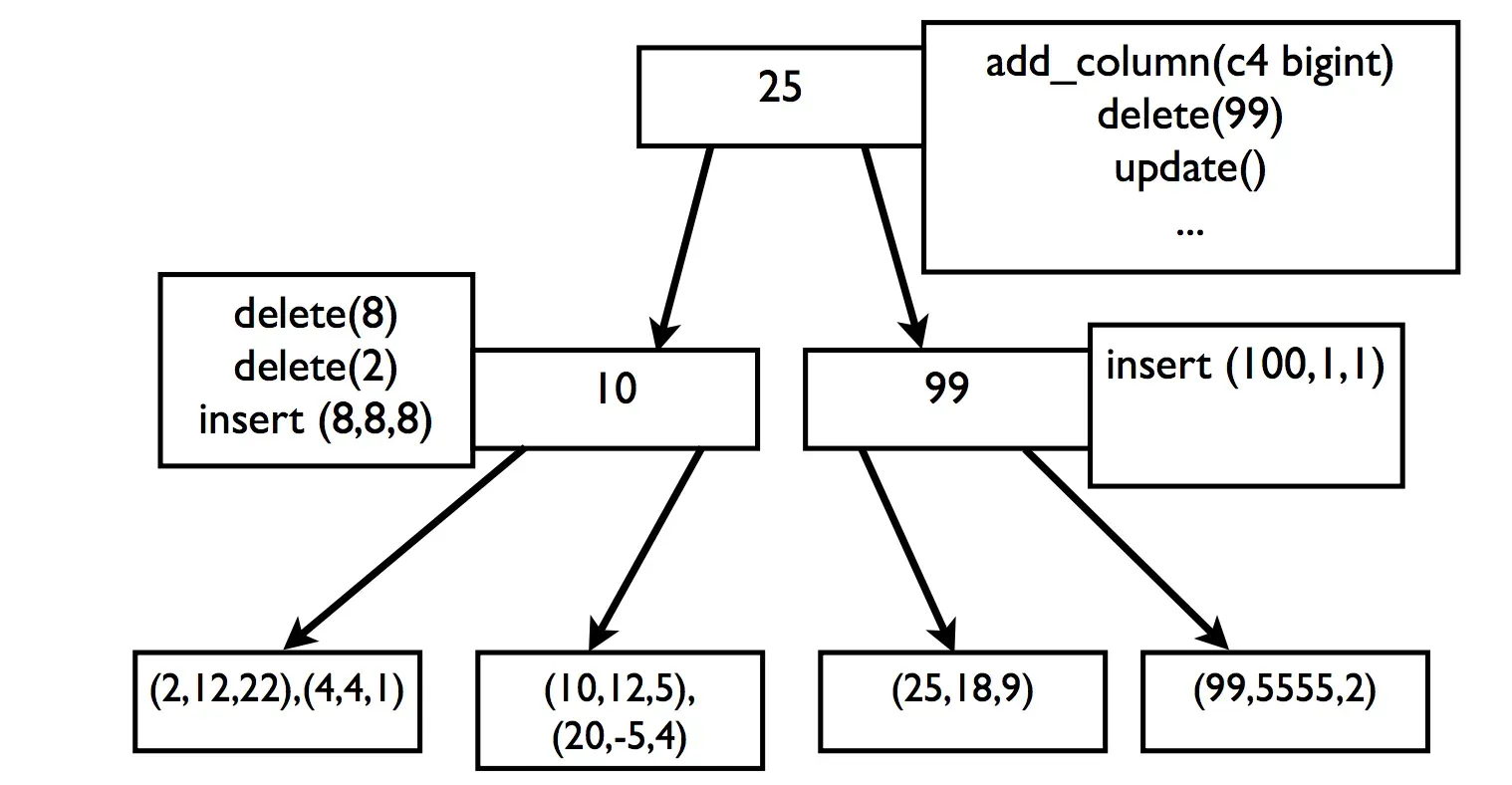
Add column, delete column, insert, update whatever operation everything is saved as message somewhere among the intermediate nodes in Fractal Tree.
The leaves still store the actual data like B Tree.
While reading, the operation has to consider all messages on its path in order to identify the actual state of the data.
Conclusion
Congrats, you made it to the end! 🎉 Either you’re truly dedicated, incredibly bored, or just scrolling aimlessly through life—no judgment. Since this was reposted from my Medium Blog , it might feel a little less spicy than usual. But hey, stick around—better, funnier, and possibly life-altering content is coming soon! (Or at least something mildly entertaining.) 😆